Accord Vision: K-Means Clustering

K-Means is one of the most popular, classic and simple approaches to clustering. Clustering is a method of unsupervised learning, and a common technique for statistical data analysis used in many fields, including machine learning, data mining, pattern recognition, image analysis and bioinformatics [3].

Download source code.

Download sample application.

The code presented here is also part of the Accord.NET Framework. The Accord.NET Framework is a framework for developing machine learning, computer vision, computer audition, statistics and math applications. It is based on the already excellent AForge.NET Framework. Please see the starting guide for mode details. The latest version of the framework includes the latest version of this code plus many other statistics and machine learning tools.

Introduction
1. Lloyd's K-Mean algorithm

Source code

Using the code

Sample application

Conclusion

Acknowledgements

References

See also

Introduction

In statistics and machine learning, k-means clustering is a method of cluster analysis which aims to partition n observations into k clusters in which each observation belongs to the cluster with the nearest mean [4]. In its most common form, the algorithm is an iterative greedy algorithm which converges to a local optimum after a certain number of iterations.

Illustration of the K-Means algorithm.

The algorithm works by first selecting k locations at random to be the initial centroids for the clusters. Each observation is then assigned to the cluster which has the nearest centroid, and the centroids are recalculated using the mean value of assigned values. The algorithm then repeats this process until the cluster centroids do not change anymore, or until the change less than a given threshold.

There are other refinements and extensions of the algorithm. The version depicted above is its most common form, also referred as Lloyd's algorithm.

Lloyd's K-Means algorithm

Place K points into the space represented by the objects that are being clustered. These points represent initial group centroids.

Assign each object to the group that has the closest centroid.

When all objects have been assigned, recalculate the positions of the K centroids.

Repeat Steps 2 and 3 until the centroids no longer move. This produces a separation of the objects into groups from which the metric to be minimized can be calculated.

Source code

The source code has been implemented using Accord.NET and is now part of the framework. In the current version (2.1.2), the following classes related to K-Means are contained inside the Accord.MachineLearning namespace. The source code available in this page contains only the parts of the framework actually needed to support the algorithm.

Class diagram for the K-Means algorithm.

The KMeans class is the main class representing the K-Means algorithm. The algorithm itself is implemented in the Compute(double[][] data, double threshold) method, which accepts a set of observations and a convergence threshold to determine when the method should stop.


/// <summary>
///   Divides the input data into K clusters. 
/// </summary>     
public int[] Compute(double[][] data, double threshold)
{
    int k = this.K;
    int rows = data.Length;
    int cols = data[0].Length;


    // pick K unique random indexes in the range 0..n-1
    int[] idx = Accord.Statistics.Tools.Random(rows, k);

    // assign centroids from data set
    this.centroids = data.Submatrix(idx);


    // initial variables
    int[] count = new int[k];
    int[] labels = new int[rows];
    double[][] newCentroids;


    do // main loop
    {

        // Reset the centroids and the
        //  cluster member counters'
        newCentroids = new double[k][];
        for (int i = 0; i < k; i++)
        {
            newCentroids[i] = new double[cols];
            count[i] = 0;
        }


        // First we will accumulate the data points
        // into their nearest clusters, storing this
        // information into the newClusters variable.

        // For each point in the data set,
        for (int i = 0; i < data.Length; i++)
        {
            // Get the point
            double[] point = data[i];

            // Compute the nearest cluster centroid
            int c = labels[i] = Nearest(data[i]);

            // Increase the cluster's sample counter
            count[c]++;

            // Accumulate in the corresponding centroid
            double[] centroid = newCentroids[c];
            for (int j = 0; j < centroid.Length; j++)
                centroid[j] += point[j];
        }

        // Next we will compute each cluster's new centroid
        //  by dividing the accumulated sums by the number of
        //  samples in each cluster, thus averaging its members.
        for (int i = 0; i < k; i++)
        {
            double[] mean = newCentroids[i];
            double clusterCount = count[i];

            for (int j = 0; j < cols; j++)
                mean[j] /= clusterCount;
        }


        // The algorithm stops when there is no further change in
        //  the centroids (difference is less than the threshold).
        if (centroids.IsEqual(newCentroids, threshold))
            break;

        // go to next generation
        centroids = newCentroids;

    }
    while (true);


    // Compute cluster information (optional)
    for (int i = 0; i < k; i++)
    {
        // Extract the data for the current cluster
        double[][] sub = data.Submatrix(labels.Find(x => x == i));

        // Compute the current cluster variance
        covariances[i] = Statistics.Tools.Covariance(sub, centroids[i]);

        // Compute the proportion of samples in the cluster
        proportions[i] = (double)sub.Length / data.Length;
    }


    // Return the classification result
    return labels;
}

The implementation is quite straightforward and does not use additional techniques to avoid convergence problems. More refined techniques may be added to the implementation in the future, so please make sure to download the latest version of Accord.NET Framework for the most up-to-date revision of the code.

Using the code

To use the code, create a new instance of the KMeans class passing the desired number of clusters to its constructor. Additionally, you may also pass a distance function to be used as a distance metric during clustering. The default is to use the square Euclidean distance.

    // Declare some observations
    double[][] observations = 
    {
        new double[] { -5, -2, -1 },
        new double[] { -5, -5, -6 },
        new double[] {  2,  1,  1 },
        new double[] {  1,  1,  2 },
        new double[] {  1,  2,  2 },
        new double[] {  3,  1,  2 },
        new double[] { 11,  5,  4 },
        new double[] { 15,  5,  6 },
        new double[] { 10,  5,  6 },
    };

    // Create a new K-Means algorithm with 3 clusters 
    KMeans kmeans = new KMeans(3);

    // Compute the algorithm, retrieving an integer array
    //  containing the labels for each of the observations
    int[] labels = kmeans.Compute(observations);

    // As a result, the first two observations should belong to the
    //  same cluster (thus having the same label). The same should
    //  happen to the next four observations and to the last three.

Sample application

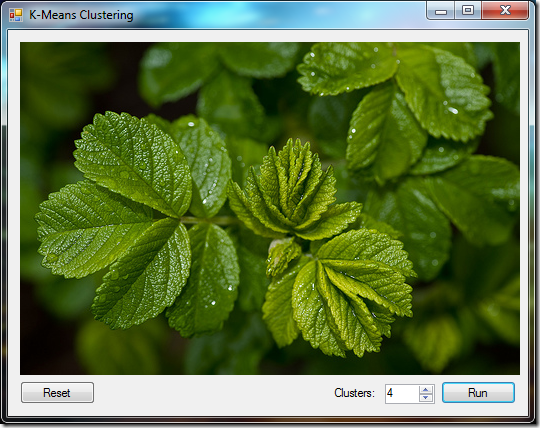
The k-means clustering algorithm is commonly used in computer vision as a form of image segmentation. The results of the segmentation are often used to aid border detection and object recognition. The sample application performs image segmentation using the standard squared Euclidean distance over RGB pixel color space. There are, however, better distance metrics to be used for image segmentation, such as weighted distances and other color spaces, which will not be addressed in this example.

Original image (from Ossi Petruska Flickr page*).

To perform image segmentation, we will first translate our image into an array of pixel values. The single image will be read, pixel by pixel, into a jagged array where each element is a double array of length 3. Each element of those double array will contain one of the three RGB values scaled to the interval [–1,1].

After we perform clustering on this array of pixel values, each pixel will have an associated cluster label. Each of these values will then be swapped by its corresponding cluster centroid. The source code below is called when one clicks the Run button in the application.

private void btnRun_Click(object sender, EventArgs e)
{
    // Retrieve the number of clusters
    int k = (int)numClusters.Value;

    // Load original image
    Bitmap image = Properties.Resources.leaf;

    // Transform the image into an array of pixel values
    double[][] pixels = image.ToDoubleArray();


    // Create a K-Means algorithm using given k and a
    //  square euclidean distance as distance metric.
    KMeans kmeans = new KMeans(k, Distance.SquareEuclidean);

    // Compute the K-Means algorithm until the difference in
    //  cluster centroids between two iterations is below 0.05
    int[] idx = kmeans.Compute(pixels, 0.05);


    // Replace every pixel with its corresponding centroid
    pixels.ApplyInPlace((x, i) => kmeans.Clusters.Centroids[idx[i]]);

    // Show resulting image in the picture box
    pictureBox.Image = pixels.ToBitmap(image.Width, image.Height);
}

After segmentation, the following resulting images can be obtained:

Same image after K-Means clustering with k = 5.

Image after K-Means clustering with k = 10.

* The sample image used above has been licensed by Ossi Petruska in a Creative Commons Attribution-NonCommercial-ShareAlike 2.0 Generic license.

Conclusion

K-Means is a very simple and popular approach to clustering. The implementation presented here is the same implementation used in Accord.NET. As it can be seem, the method can be easily extended with custom distance functions through delegates or lambda expressions, and can be used in different contexts, such as image segmentation, without further modifications. As a suggestion for improvement, the method can be further speeded up by using the triangle inequality as suggested on the paper "Using the triangle inequality to accelerate k-means", by Charles Elkan.

In the next article, we will see how we can use K-Means to initialize the Expectation-Maximization algorithm for estimating Gaussian Mixture densities in Gaussian Mixture Models. Those articles will form the basis for Continuous density Hidden Markov Models.

Acknowledgements

To Antonino Porcino, who provided the first version of the code and for the valuable information about many other methods and algorithms.

References

[1] Matteo Matteucci. “Tutorial on Clustering Algorithms,” Politecnico di Milano, http://home.dei.polimi.it/matteucc/Clustering/tutorial_html/kmeans.html (acessed October 4, 2010).

[2] Teknomo, Kardi. "K-Means Clustering Tutorials," http://people.revoledu.com/kardi/ tutorial/kMean/ (acessed October 6, 2010).

[3] Wikipedia contributors, "Cluster analysis," Wikipedia, The Free Encyclopedia, http://en.wikipedia.org/wiki/Cluster_analysis (accessed October 4, 2010).

[4] Wikipedia contributors, "K-means clustering," Wikipedia, The Free Encyclopedia, http://en.wikipedia.org/wiki/K-means_clustering (accessed October 4, 2010).

Accord Vision

Tuesday, 5 October 2010

K-Means Clustering

Contents